Symbolic Execution:从思维上理解符号执行
符号执行作为软件分析、漏洞发掘领域经常出现的技术,国内已经有不少文章总结讨论。但新手直接翻阅学习这些总结性质的文章时碰到的诸如“符号路径约束”、“约束求解”、“执行状态”等专有名词会难以理解,思维逻辑与理论概念不易同轨。本文从国外的一些热门教程入手, 将符号执行从思维上捋一遍, 诠才末学,仅做抛砖引玉之用。
1. 引子:
1.0 一个样例
从一段经典的代码入手,解释符号执行的核心思路。

分析目标:对于任意可能的输入组合(a,b),找到使得断言assert语句失败的所有输入。
对于以上函数,如果使用随机测试的方法,共有2^32^×2^32^种输入组合,想要找到所有的符合条件的输入就得遍历所有输入,显然,这么做效率低下,费时费力。
符号执行的核心思想有以下几点:
- 每一个输入变量都被映射为了一个符号,例如int i ——> α
i; - 每一个符号代表所有可能的输入值的集合,例如 α
i∈[0,2^32^-1] ; - 程序中的语句都由符号来完成运算,例如i*2 + 5 ——> 2· α
i+ 5 ;
如果遇到了分支条件,需要考虑每一个分支下可能执行的路径:
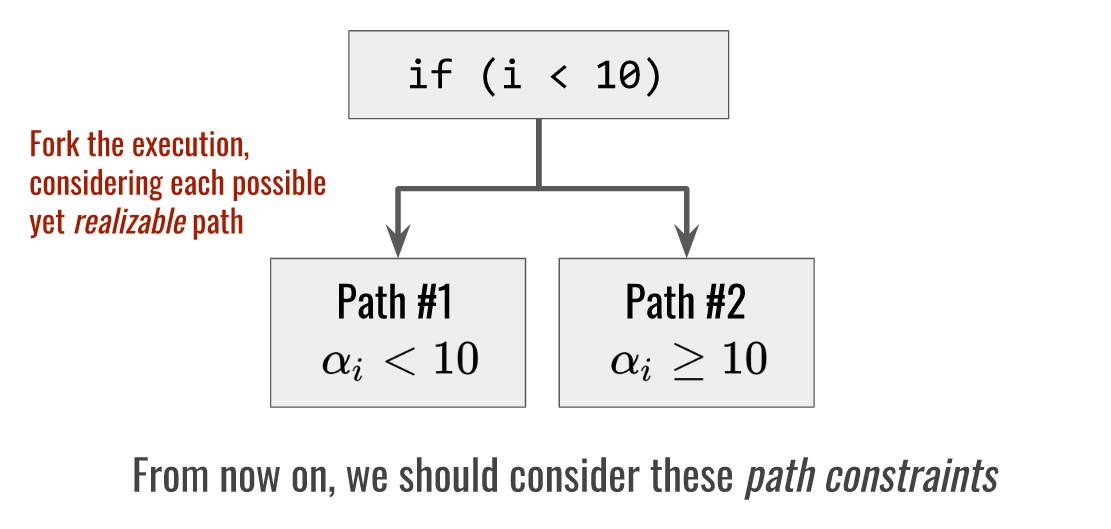
在开始第一次符号执行演练之前,这里定义执行状态(Execution state)的概念:
$$
Execution\enspace state={stmt,\sigma,\pi}
$$
- stmt是当前状态的下一个状态;
- σ是将程序变量映射到符号或者常数的映射,如果变量的值不确定就是映射到符号,反之映射到常量;
- π表示路径上的限制,即到达当前状态需要什么限制条件。例如对于上述函数,只有a^(!b)才能到达第6行,所以若程序在第6行的π = $(\alpha_a \neq 0 )\and (\alpha_b = 0)$,π的初始值为true。
如果使用符号执行来分析上述函数,在程序的开头,会得到第一个执行状态。根据上述定义,其stmt是它的下个待分析状态,也就是程序的第二行:“int x = 1, y = 0;”;其σ会将第一行引入的变量a,b映射到符号,由于a,b是输入,都不是常量,故可以得到:$\sigma={a\rightarrow \alpha_a, b\rightarrow \alpha_b}$;1开始并没有遇到条件判断语句,故π为初始值true。如下图所示:
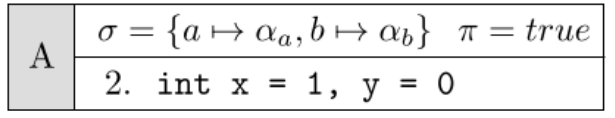
当状态A接着执行,我们遇到了一个整型声明语句,其添加了两个新变量x,y并赋初始值。故从状态A到状态B其σ添加了新的映射,stmt变为下一条待执行语句,π不变:

从状态B的stmt表明接下来的分析遇到了条件判断语句,对于if语句的两种可能,衍生出两个执行状态:
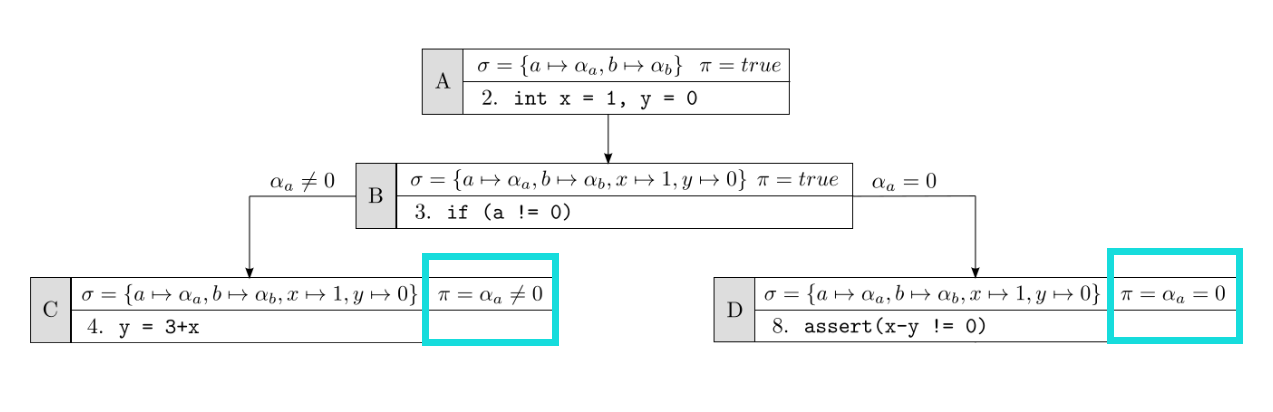
当状态D继续执行就遇到了assert断言语句,在断言处我们判断当前的条件(σ、π)下是否满足断言条件:
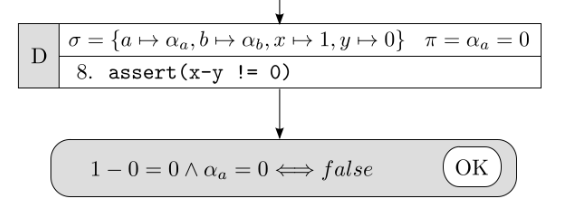
如图所示,在x = 1,y = 0,且αa = 0的条件下,x-y ≠ 0 ,断言并未触发,此条分支执行结束。
当C状态继续执行,遇到了y = 3 + x赋值语句,这时就要改变σ中的映射关系:
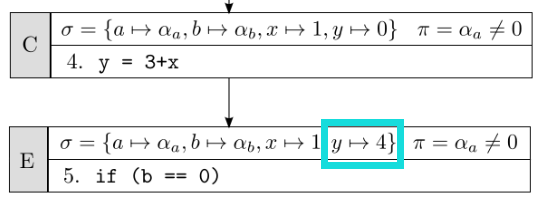
状态E继续执行,遇到条件判断语句,同理,生成两个分支:

状态G进行逻辑判断,并未触发:

状态F继续执行,进行判断,触发错误条件:
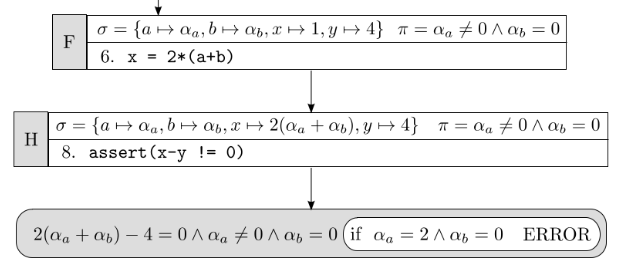
到此为止,所有分支执行完毕,符号执行判断出当a=2且b=0时,断言语句会被触发。如果我们的测试目标从触发断言语句改为触发漏洞行为,符号测试就是进行漏洞的排查。

1.1 机器如何判断?
上文所述的例子描述了符号执行的基本逻辑:用符号代替变量,判断最终生成的布尔表达式是否可满足。在上文中,我们当然可以轻松地用大脑分析出只要输入a = 2且b = 0,断言就会被触发。但在面对复杂且庞大的逻辑表达式时,我们不能每次都去人工分析,想要完整的利用计算机实现符号执行,就需要解决自动化判断逻辑表达式是否可满足的问题。
SAT,布尔可满足性问题,它询问给定布尔公式的变量是否可以用值TRUE或FALSE一致地替换,以使该公式的值为TRUE。例如$a\and b $就是可满足的,而 $a \and !a$ 就是不可满足的。SAT在理论上已经被证明是NP问题,虽然可以快速验证这个问题的解,但不能确定其求解速度。目前已经有很多成熟的SAT算法。
SMT将SAT实例中的一些二进制变量(True or False)替换为非二进制变量,非二进制变量包括线性不等式(x+2y > 4)、符号等式($f(f(u,v),v) = f(u,v)$)。SMT的背景符合符号执行所面临的的问题,利用已有的SMT解法就可以解决上述的逻辑表达式自动化判断问题。可以看到,我们将符号执行过程中的一系列限制条件称为约束(constraint),而使用SMT对该约束进行求解的过程就叫约束求解。
使用符号执行不并一定要具体的理解SMT的技术细节,但其逻辑大体如下:
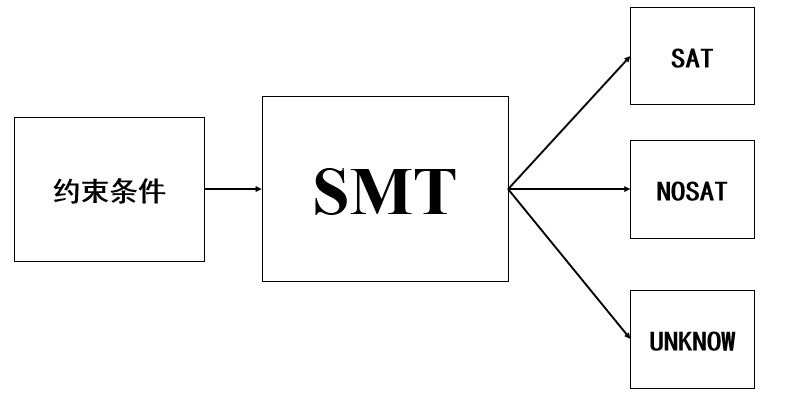
对于SMT这类NP完全问题,在指定时间内SMT求解器会给出是否满足的结果,若超出时间则给出“不知道”。
综上,在使用前文定义的符号执行流程分析后,配合SMT Slover即可进行完整的符号执行分析。
1.2 如何证明没有其它样例?
如何证明我们找到的”a=2且b=0”就是所有的满足条件的输入了?
从理论上来说,符号执行遍历执行了程序所有可能的条件分支,分析了所有可能路径下的SMT问题,以此得出的结果必然是完整的,没有其它特例的。但在实际应用中,存在一些很难被解决的限制,执行生成的路径可能特别多,并且影响程序执行路径的因素不再是a,b几个变量这么简单,这些因素导致了在实际的符号执行中不便于做理论完整的评估。
2. 进一步深入
2.1 memory model
看看如下代码:

当代码中涉及到对内存的操作时,又如何设计相应符号呢?事实上我们将整个内存看成一个大数组MEM[],对内存的操作不过是对数组的操作:

这里的y1与y不完全相同,y代表地址,y1代表MEM数组中的位置。在C语言中,y = x + 10其实是y指针往后移动了10个x指针类型的位置,也就是y1 = x1 + 10*sizeof(int)。而对于malloc函数,可以将其简单看做返回未使用空间起始地址的函数,下面是一个简单的抽象:

当将堆内存抽象为数组操作时,现有SMT求解器支持基于数组的逻辑操作(Theory of arrays)。对数组的操作可以抽象为:
$$
\begin{equation}
a{i\rightarrow e}[k] = \left{
\begin{array}{cl}
a[k] & if & k \neq i \
e & if & k = i
\end{array} \right \
\end{equation}
$$
经过一系列的数组操作:
$$
a{i\rightarrow 5}{j\rightarrow 7}···[k] = 5 \Leftrightarrow ···
$$
SMT引擎会将数组操作转化为对应的布尔操作,进而进行求解。当然,这个函数与C语言中malloc具体实现很不一样,其忽略了很多细节,例如对当前分配空间是否使用的检查。但经过这样简单的抽象,就可以使用上述的思路进行符号执行的判断。
**memory model,翻译为“内存建模”,从以上的例子可以看出,面对复杂的数据结构、函数操作甚至是陌生的第三方库,在使用符号执行前需要对其进行合适的抽象建模。**目前已经有许多研究成果针对C语言的第三方库建模。建模的好坏也直接影响符号执行的性能与效率,例如对于上述的malloc,如果我们仅仅想检测最简单的缓冲区溢出漏洞,考虑malloc复杂的堆分配机制就是多余的。

2.2 path explosion
抛开上述举例的toy code,现实中需要检测的商业软件一般都有成千上万行代码,其结构包含大量分支、循环、内存操作等等,如果还按照上文的思路进行执行,不仅会导致搜索时间的过长,还会使最终的执行状态过大。
在设计符号时,就应该避免引入无关/作用不大的符号,避免状态过大。且在路径搜索时可以使用深度优先、随机路径、广度优先、错误路路径优先等算法优化搜索方法,以求达到广度与深度的平衡。(又是经典的exploration and exploitation问题)
具体的进一步深入可以查看:Baldoni R, Coppa E, D’elia D C, et al. A survey of symbolic execution techniques[J]. ACM Computing Surveys (CSUR), 2018, 51(3): 1-39.
3. 实践一下
对于源代码分析,KLEE[4]是很个很棒的框架工具;对于二进制分析,S2E[5]是个非常强有力工具,但使用稍显复杂。
这里使用angr,angr[6]是一个分析二进制的python框架,使用非常便捷。
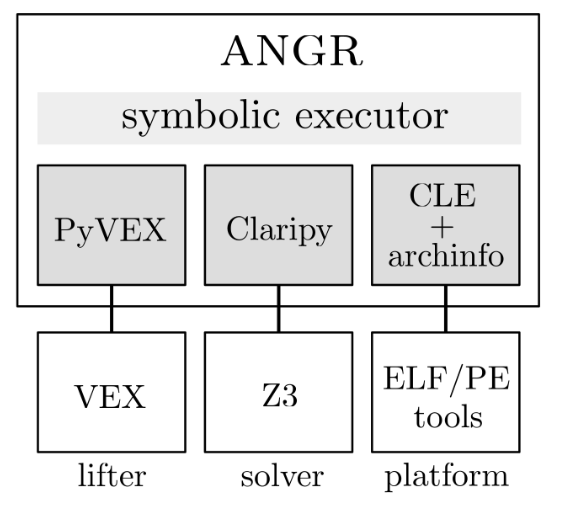
**目标1:**使用angr符号执行分析本文举出的第一个例子,follbar()的二进制文件.
**目标2:**使用angr符号执行分析logic-bomb二进制程序.
安装相应虚拟环境:
#安装python虚拟环境
sudo pip3 install virtualenvwrapper
#创建目录用来存放虚拟环境
mkdir $HOME/.virtualenvs
#在~/.bashrc中,最后添加
export WORKON_HOME=$HOME/.virtualenvs
VIRTUALENVWRAPPER_PYTHON=/usr/bin/python3
source /usr/local/bin/virtualenvwrapper.sh
#创建一个名为angr的虚拟环境
mkvirtualenv angr
#进入虚拟环境并安装angr
workon angr
pip3 install angr
3.1 foolbar
使用idafree-7.0打开slide-example/example文件,找到foolbar函数:

打开行前缀选项:Options–>General–>Disassembly–>Line prefixes(graph),可以显示汇编指令地址:
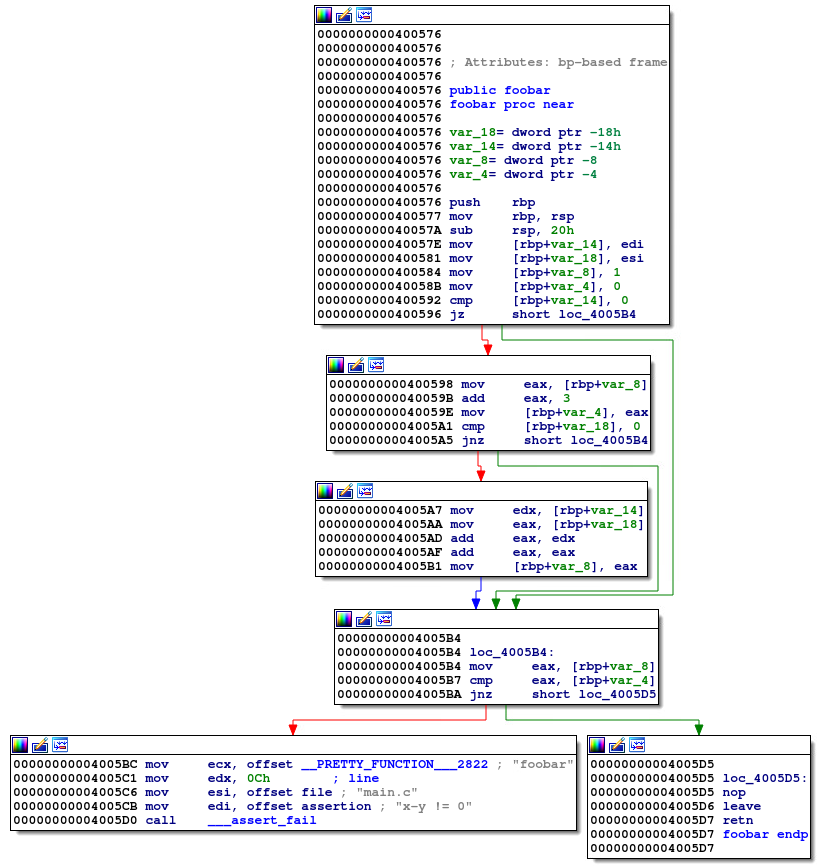
想要使用angr分析函数,需要给定其:
- start target:代码开始运行地址;
- find target:代码结束运行地址;
- avoid targets:哪些路径(地址)被忽略,以此来避免路径爆炸问题;

由于angr不知道什么是符号什么是常数,后续还需要定义输入的符号。angr分析脚本如下:
import angr
proj = angr.Project('example')
# customize XXX, YYY, and ZZZ!!!
start = XXX # addr of foobar
avoid = [YYY] # point(s) that are not interesting (e.g., early exits)
end = ZZZ # point that I want to reach
# blank_state since exploration should start from an arbitrary point
# otherwise, use entry_state()
state = proj.factory.blank_state(addr=start)
# arguments are inside registers in x86_64
a = state.regs.edi
b = state.regs.esi
sm = proj.factory.simulation_manager(state)
while len(sm.active) > 0:
print(sm) # get a feeling of what is happening
sm.explore(avoid=avoid, find=end, n=1)
if len(sm.found) > 0: # Bazinga!
print("\nReached the target\n")
state = sm.found[0]
print("%edi = " + str(state.solver.eval_upto(a, 10)))
print("%esi = " + str(state.solver.eval_upto(b, 10)))
break 代码整体很简洁,angr.Project构建Project类,Project类是angr模块的主类,它对一个二进制文件进行初始的分析以及参数配置,并将数据存储起来进行后续进一步分析。proj.factory.blank_state()指定任意地址开始运行。在Angr中,程序每执行一步(也就是step)就会产生一个状态(state,在SM这里叫做stashe),Simulation_Manager就是提供给我们管理这些state的接口。注意到,符号变量是使用寄存器进行存储的。
运行脚本:
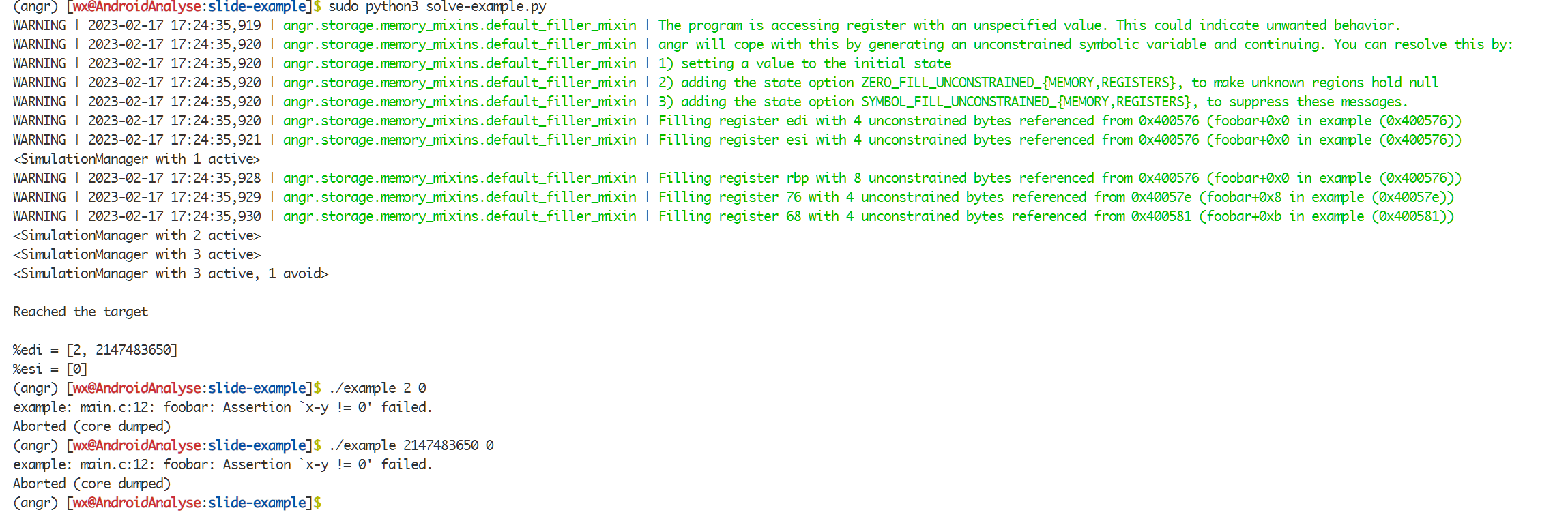
可以看到,脚本程序分析出,当edi(a)=2或者2147483650,esi(b)=0时会触发断言,这里2147483650显然就是整数溢出后的2。以此可见符号执行的程序实现需要考虑到计算机数字与数学数字的区别。
3.2 logic-bomb
logic-bomb是一个没有源码的二进制程序,你需要依次输入正确答案以此逃过爆炸:

用IDA打开:
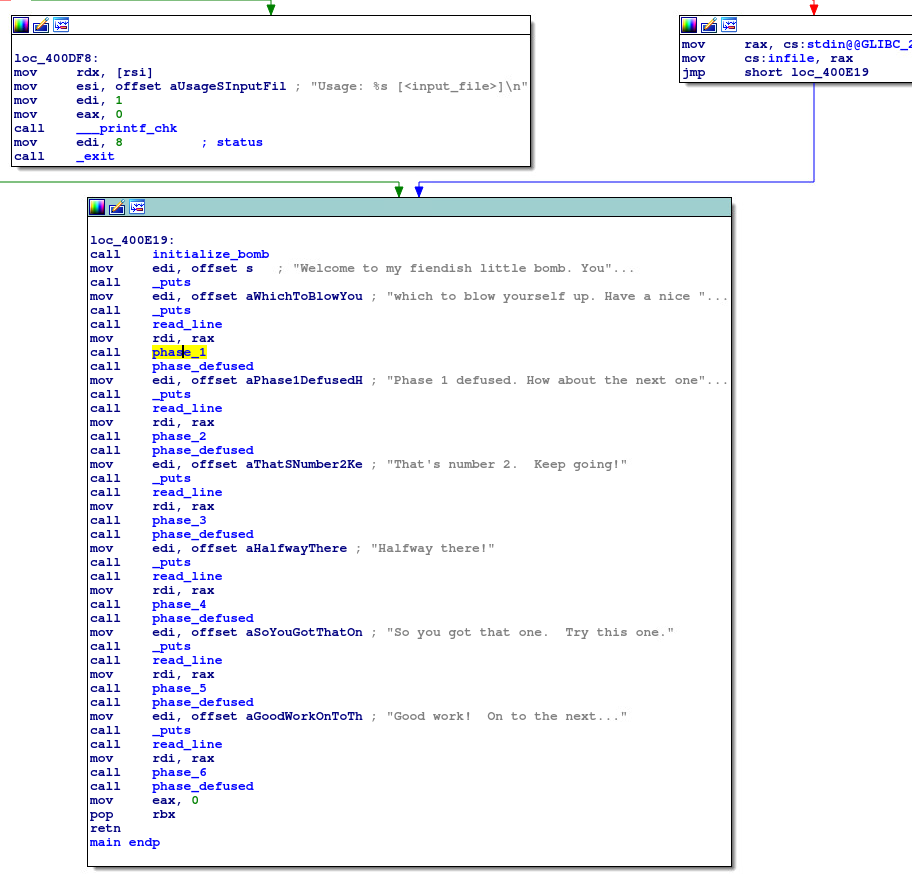
可以看到程序从主函数开始分别调用phase_1()、phase_2()······phase_6(),进入phase_1():
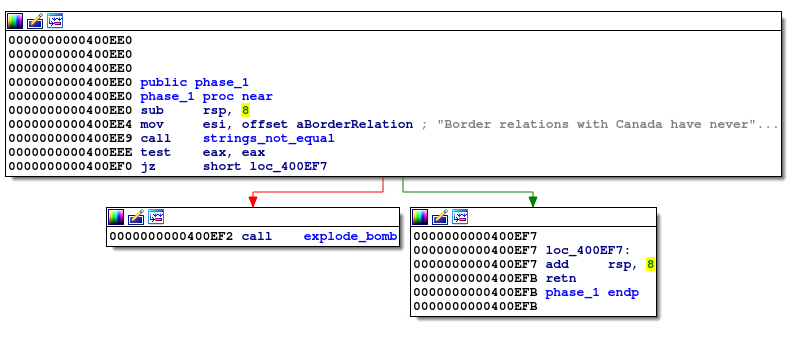
如果你懂得逆向的知识,可以尝试人工分析去解开这个bomb,但如果使用符号执行分析,只需要确定使其成功通过的地址即可:
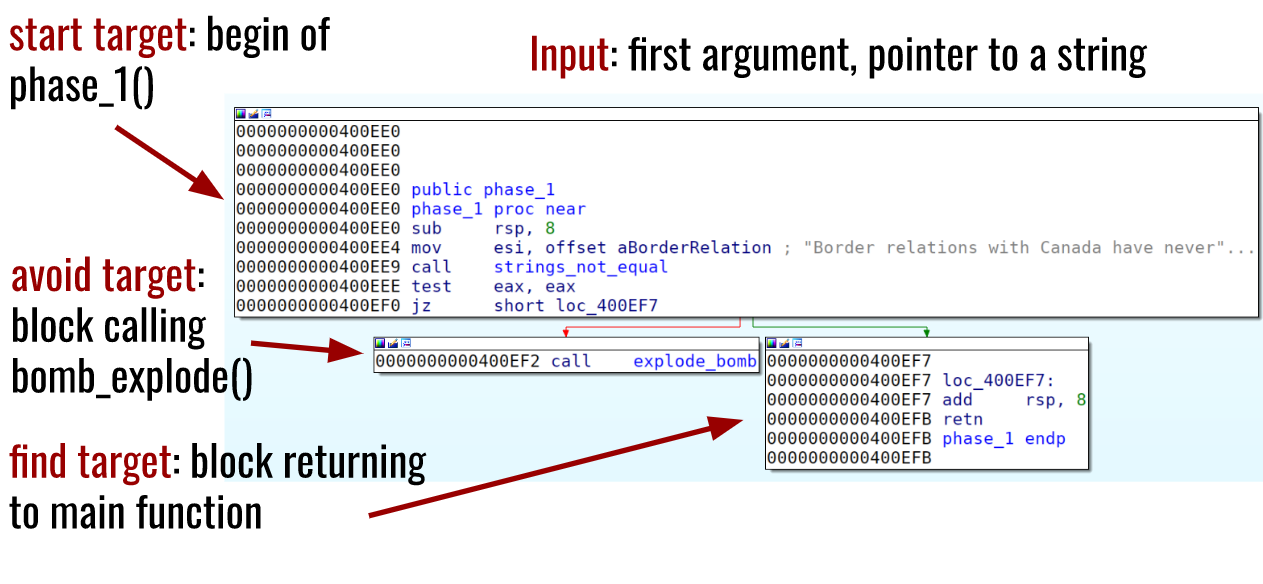
分析脚本如下:
import angr
import logging
import claripy
import pdb
import resource
import time
proj = angr.Project('bomb')
start = XXX
avoid = [YYY]
end = [ZZZ]
state = proj.factory.blank_state(addr=start)
# a symbolic input string with a length up to 128 bytes
arg = state.se.BVS("input_string", 8 * 128)
# an ending byte
arg_end = state.se.BVS("end_input_string", 8)
# add a constraint on this byte to force it to be '\0'
state.se.add(arg_end == 0x0)
# the constraint is added to the state.
# Another way to do same is with:
# arg_end = state.se.BVV(0x0, 8)
# in this case arg_end is a concrete value
# concat arg and arg_end
arg = state.se.Concat(arg, arg_end)
# an address where to store my arg
bind_addr = 0x603780
# bind the symbolic string at this address
state.memory.store(bind_addr, arg)
# phase_one reads the string [rdi]
state.regs.rdi = bind_addr
# make rsi concrete
state.regs.rsi = 0x0
pg = proj.factory.simulation_manager(state)
start_time = time.time()
while len(pg.active) > 0:
print(pg)
# step 1 basic block for each active path
pg.explore(avoid=avoid, find=end, n=1)
# Bazinga!
if len(pg.found) > 0:
print()
print("Reached the target")
print(pg)
state = pg.found[0]
sol = state.solver.eval(arg, cast_to=bytes).decode('ascii').split('\0')[0]
print("Solution: " + sol)
break
print()
print("Memory usage: " +
str(resource.getrusage(resource.RUSAGE_SELF).ru_maxrss / 1024) + " MB")
print("Elapsed time: " + str(time.time() - start_time)) 执行脚本:
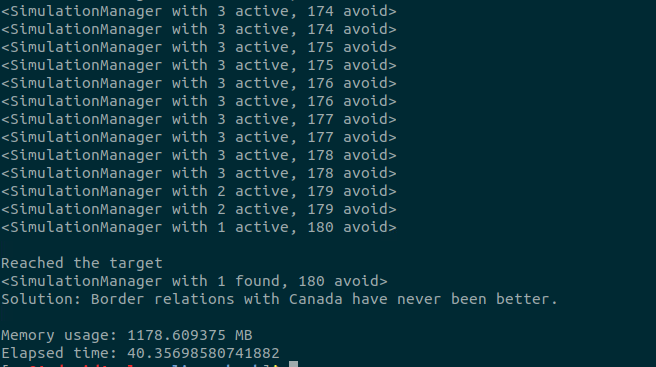
可以看到,符号执行仅用40秒就找到了phase1()的口令:“Border relations with Canada have never been better.”

对于phase_2()······phase_6()使用同样的方法即可破解,这里略。
综上,我们可以看到符号执行在面对复杂的二进制文件时卓越的能力表现,在logic-bomb中,其二进制文件并没有经过混淆处理,相应的函数名,完整字符串都可以经过IDA分析后直接看到,所以对logic-bomb人工分析其实也并不复杂。但在真实的软件测试环境里,大量的二进制文件都是经过混淆加壳处理的,人工分析无法直接定位关键函数的作用(logic-bomb直接用函数名体现了函数的作用),甚至定位函数的进出口都变得具有挑战性,这时符号执行的优越性就有更明显的体现。
参考:
[2] symbolic-execution-tutorial/README.md at master · ercoppa/symbolic-execution-tutorial (github.com)
[3] MIT 6.858 Computer Systems Security, Fall 2014—–10. Symbolic Execution
[4] KLEE
[5] Overview - S²E: A Platform for In-Vivo Analysis of Software Systems (s2e.systems)
[6] angr
